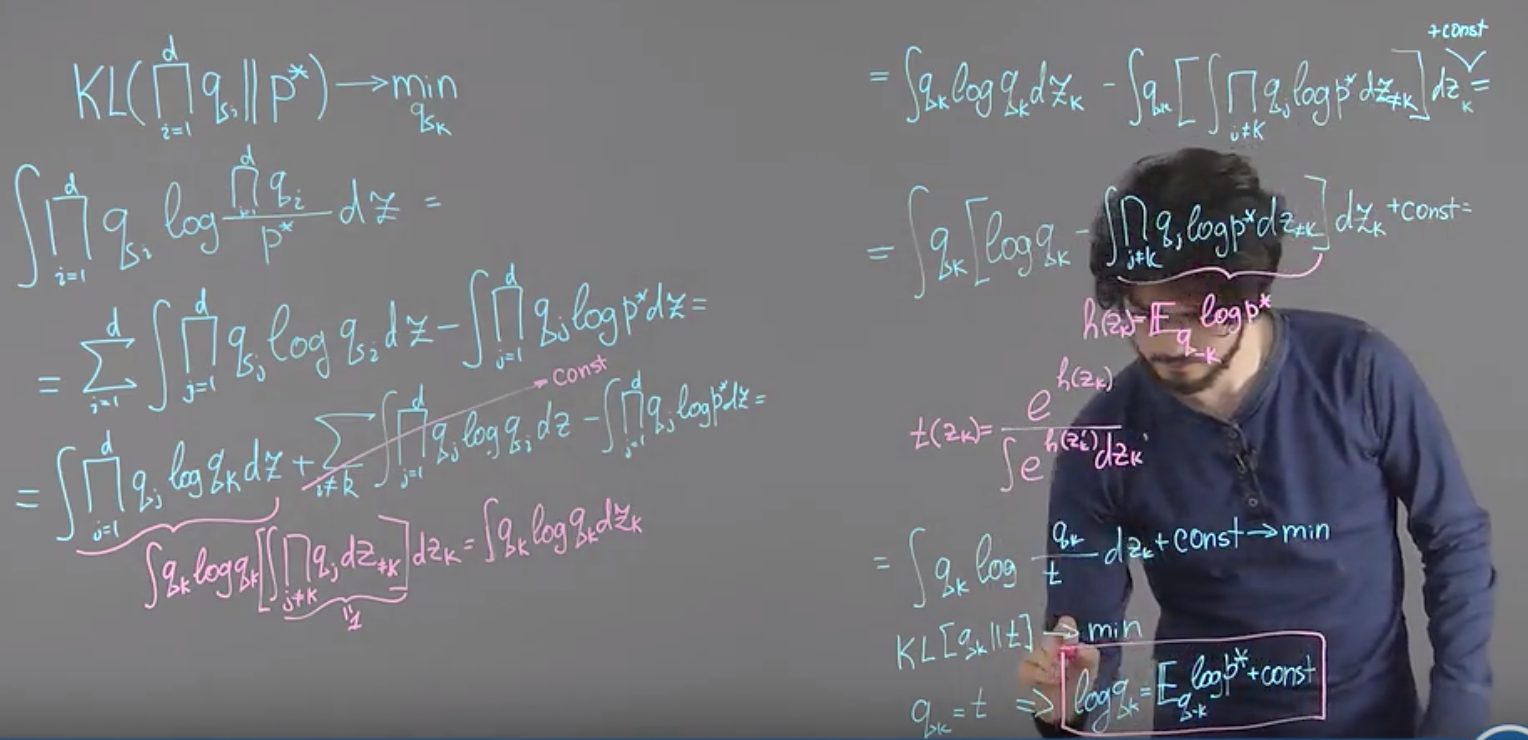Why approximate inference?
Variational inference는 posterior을 근사하는 방법이다.
Analytical inference가 있는데 왜 근사해야할까?
conjugate prior의 경우는 계산이 쉽지만, 많은 경우에 그렇지 않은 경우가 많고 그러면 posterior를 계산하기 어려워진다.
예를 들면 week 5에서 배우게될 variational autoencoder의 경우 likelihood가 neural network로 되어있어서 conjugacy가 없고, bayes formula로 posterior를 계산할 수 없다.
그런데 정확한 포스테리어 분포가 꼭 필요할까?
실용적으로는 비슷한 분포를 사용해도 좋은 성능을 낼 수 있다.
이 때 full posterior를 가장 잘 근사하는 분포를 찾아내는 것이 variational inference이다.
Variational inference

2는 KL divergence를 최소화하는 것을 말한다.
Choice of variational family
Q가 너무 작으면 full posterior가 포함되지 않는데, 이 때 Q와 p*의 거리가 KL divergence이다.
그러나 Q가 너무 크면 variational inference를 계산하기 힘들어진다.
이 때는 bayes formula만을 사용할 수 있지만, 이것이 어려운 경우가 많기 때문이다.
Unnormalized distribution

p(X)때문에 정확한 값의 계산은 어려운데, 이를 normalizing 요소로 잡으면 KL divergence의 log에서 constant로 빠져나오고, minimize할 대상은 p*(z)에 비례하는 p^(z)와 q(z)의 KL divergence임.
Mean field approximation
Optimization

q를 각 qi의 곱으로 표현하고, 각 qi에 대해 coordinate descend하는 과정을 통하여 KL divergence를 최소화한다.