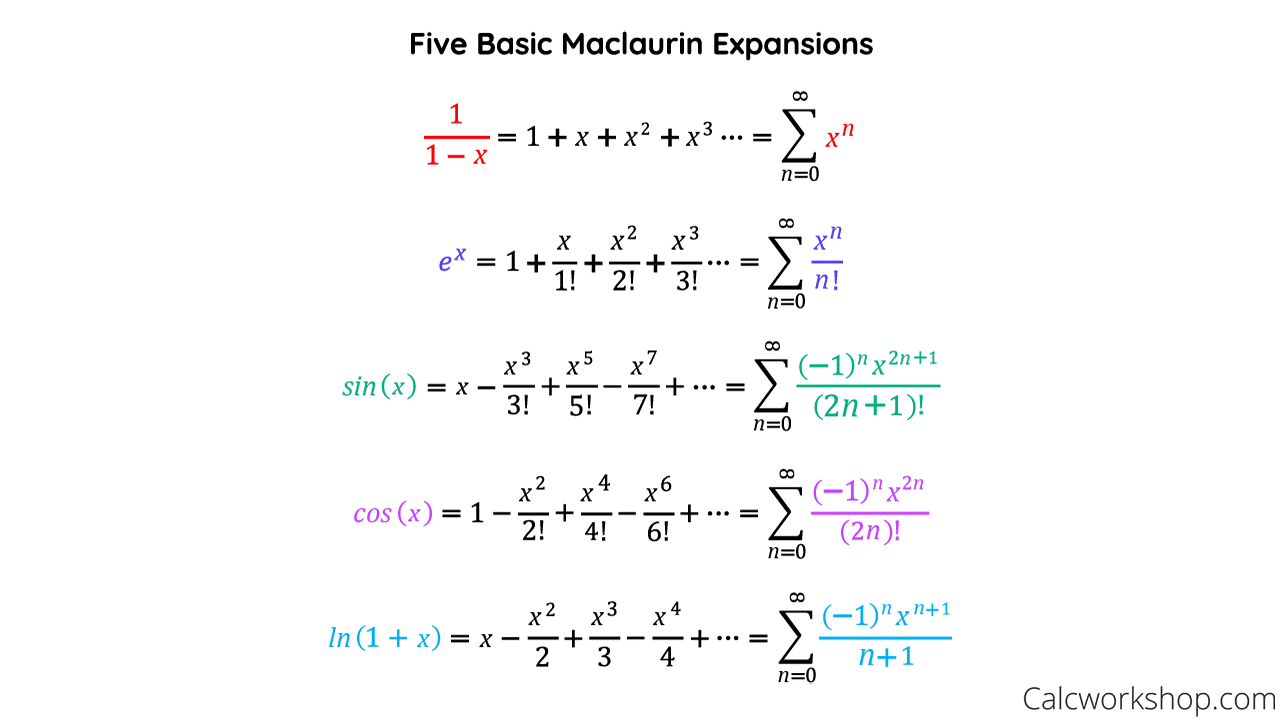미분
근방
\(x_0\)의 \(\epsilon >0\) 근방
\[\{x| \left| x-x_0 \right| < \epsilon \}\]개구간
\(A: (a,b)\) 개구간의 경우
\[x \in A\]유계집합(bounded set)
원점으로 부터의 거리가 유한한 집합.
Squeeze Theorem
\[g(x) \le f(x) \le h(x)\] \[lim_(x \rightarrow c)g(x) = lim_(x \rightarrow c) h(x)=k\]일 때,
\[lim_(x \rightarrow c)f(x)=k\]중간값 정리
연속함수가 갖는 특징이다.
\(f:[a,b] \rightarrow R\)
\(f(a) < f(b)\)
일 때,
\(f(a) \le m \le f(b)\) 라고 하면
\(a < c < b\) 에 대해 \(f(c)=m\) 이 되는 어떤 c가 존재한다.
Mean Value Theorem
\(f:(a,b) \rightarrow R\): 미분가능
\[c_1,c_2(c_1 < c_2)\] \[f(c_2)-f(c_1)=f'( \xi )(c_2-c_1), \exists \xi \in [c_1,c_2]\]이를 다시 쓰면,
\[\frac{f(c_2)-f(c_1)}{c_2-c_1}=f'(\xi)\]평균변화율이 도함수와 같다.
대역적인 정보와 국소적 정보가 연결되는 것이 의미이다.
연쇄법칙
\[y=(g \cdot f)(x)\] \[\frac{dy}{dx}=(g \cdot f)'(x)=g'(f(x)) \cdot f'(x) \\\\ =g'(u) \frac{du}{dx}=\frac{dy}{du} \cdot \frac{du}{dx}\]중간에 f를 u로 치환하였다.
\[u=f(x), y=g(u)\]역함수의 도함수
\[(f^{-1} \cdot f)(x)=x\] \[y=f(x) \rightarrow x=f^{-1}(y)\] \[(f^{-1}))'(f(x)) \cdot f'(x)=1\] \[(f^{-1})(y) \cdot f'(x)=1\] \[\frac{dx}{dy} \cdot \frac{dy}{dx}=1\] \[\frac{dx}{dy}=\frac{1}{\frac{dy}{dx}}\]L’hospital rule
\[lim_{x \rightarrow 1} \frac{(x-1)^2}{x-1}\]위와 같은 식은 \(\frac{0}{0}\) 꼴으로 가는데, 이를 부정형이라고 한다.
\[lim_{x \rightarrow \infty} \frac{x^2}{x}\]이것도 \(\frac{\infty}{\infty}\) 부정형이다.
부정을 유발하는 인수를 나눠서 없앨 수 있으면 없애면 되지만, 그러기 힘든 경우도 많다.
만약 f,g가 모두 미분가능하고,
\[lim_{x \rightarrow a}g'(x) \ne 0\] \[lim_{x \rightarrow a}\frac{f(x)}{g(x)} = lim_{x \rightarrow a}\frac{f'(x)}{g'(x)}\]여기서 a가 무한대로 발산해도 성립한다.
테일러 전개를 통해 증명할 수 있다.
0/0, 무한/무한 꼴의 부정형일 때 사용할 수 있다.
Fermat theorem
연속함수에서 극값이면 도함수가 0이된다.
역은 성립하지 않는다.
역의 경우 이계도함수를 통해 판정할 수 있다.
의미
도함수를 통해 선형화를 하는 것이 가능하고, 선형화를 통한 Analysis, 최대최소값 문제 해결, 그리고 최적화를 하는데에 필수적이다.
적분
부정적분
어떤걸 미분하면 이 함수가 나오는가?
미분의 역연산
상수 생성!
부분적분
\[\int f'(x)g(x)dx = f(x)g(x) - \int f(x)g'(x)dx\]곱함수의 미분의 역연산을 통해 유도 가능.
치환적분
\[\int f(g(x))g'(x)dx=\int f(t)dt, t=g(x)\]다음처럼 하면 나옴.
\[\frac{dt}{dx}=\frac{dg}{dx}\] \[\int f(t)\frac{dt}{dx} dx=\int f(t)dt\]연쇄법칙을 통해서 유도 가능.
정적분, 리만적분
리만합의 극한을 통해 정적분 유도 가능.
“그래프 아래의 면적”
극곡선의 길이
\[r=f(\theta), a \le \theta \le b\]극곡선을 나타내는 다음 관계식 벡터를 정의할 수 있다.
\[\alpha (\theta) = < rcos \theta, rsin\theta >\]\(r=f(\theta)\) 이므로,
\[< f(\theta) cos\theta, f(\theta) sin\theta >\] \[alpha'(\theta)=< f'(\theta)cos\theta-f(\theta)sin\theta, f'(\theta)sin\theta + f(\theta)cos\theta >\] \[L=\int_{a}^{b} |\alpha'(\theta)| d\theta\] \[|\alpha'(\theta)|=\sqrt{(f(\theta))^2+(f'(\theta))^2}\] \[L=\int_{a}^{b} \sqrt{(f(\theta))^2+(f'(\theta))^2} d\theta\]극곡선의 넓이
영역의 넓이를 부채꼴 넓이로 근사하고 각도를 0에 가깝게 작게하면 에러가 0으로 수렴함.
수열과 급수(Sequence and Series)
적분비교판정법
무한급수의 수렴여부를 적분을 통해 알아보는 방법.
교대급수판정법
부호가 +- 번갈아가며 나타나는 수열의 급수를 말한다.
부호를 통일하였을 때(절대값) 크기가 monotonic하게 줄어들면서 0으로 수렴하면 교대급수도 수렴한다.
비판정법(Ratio test)
멱급수의 수렴성을 조사하는데 매우 탁월하다!
다음 항과 이전항의 비의 절대값이 1보다 작을 때, (점점 작아질 때) 급수는 절대수렴하고,
다음 항과 이전항의 비의 절대값이 1보다 클 때, (점점 커질 때) 급수는 절대발산한다.
만약 다음항과 이전항의 비가 같을 때, 이 방법으로는 판정할 수 없다.
멱급수(Power series)의 수렴과 미분과 적분
\[\sum_{n=0}^{\infty}a_n(x-a)^n\] \[=a_0 + a_1(x-a) + a_2(x-a)^2+...\]이러한 것을 멱급수라고 한다. 항이 무한하다.
비판정법을 통해 수렴성을 체크.
미분과 적분
\[f(x)=\sum_{n=0}^{\infty}a_n(x-a)^n, |x-a|<R\]여기서 R이 수렴반경.
미분
\[f'(x)=\sum_{n=0}^{\infty}n(a_n)(x-a)^{n-1}, x \in(a-R, a+R)\]적분
\[\int f(x)dx=(\sum_{n=0}^{\infty} a_n \frac{(x-a)^{n+1}}{n+1}) +C\]이게 왜 가능하지?
수렴반경은 미분을 하든 적분을 하든 동일하기 때문에 가능한것이다.
Taylor Series, Maclaurin Series
어떤 함수가 멱급수로 표현되면, 그 표현은 유니크하다.
그러나 모든 함수를 멱급수표현 할수 있는 것은 아니며, 모든 차수의 도함수가 존재하더라도 그럴 가능성이 있다.
그러나 일반적으로 배우는 삼각함수, 지수함수, 대수함수, 역삼각함수, 다항함수, 유리함수들은 모두 멱급수 전개가 가능하다.
\[f(x)=a_0+a_1(x-a)+a_2(x-a)^2+\cdots\] \[f'(x)=a_1+2 \cdot a_2(x-a) + 3 \cdot 2 \cdot a_3(x-a)^2+ \cdots\]이를 통해 계수를 정리하면
\[a_0=f(a)\] \[a_1=f'(a)\] \[a_2=f''(a)/2!\] \[a_3=f'''(a)/3!\]일반항으로 표현하면
\[a_n=\frac{f^{(n)}(a)}{n!}\]Taylor series
\[\sum_{n=0}^{\infty}a_n(x-a)^n = \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!}\]f(x)=exp(x)
\[f(x)=e^x\]x=1에서
\[f(x)=\sum_{n=0}^{\infty} \frac{f^{(n)}(1)}{n!} (x-1)^n\]\(f^{(n)}=e^1=e\) 이므로,
\[f(x)=\sum_{n=0}^{\infty} \frac{e}{n!}(x-1)^n\]Maclaurin series
\[\sum_{n=0}^{\infty}a_n(x)^n = \sum_{n=0}^{\infty} \frac{f^{(n)}(0)}{n!}\]f(x)=exp(x)
\[f(x)=e^x\]x=0에서
\[f(x)=\sum_{n=0}^{\infty} \frac{f^{(n)}(0)}{n!} x^n\] \[f(x)=\frac{f(0)}{0!} + \frac{f'(0)}{1!}x + \frac{f''(0)}{2!}x^2 + \frac{f'''(0)}{3!}x^3+ \cdots\]\(f^{(n)}=e^0=1\) 이므로,
\[f(x)=\sum_{n=0}^{\infty} \frac{1}{n!}x^n\]근사값
a 근방에서 테일러 급수는 원래 함수와 근사한다.
테이블