Gambler’s Ruin
A와 B 두 명의 도박꾼이 매 라운드 $1씩 걸고 도박을 한다.
이긴 사람이 상대방의 $1을 가져가고, 둘 중 한명이 가지고 온 돈이 바닥날 때까지 이 과정을 반복한다.
이를 수학적으로 모델링하면,
p=P(A가 어떤 라운드를 이긴다)
q=1-p
A는 i달러, B는 N-i 달러를 가지고 게임을 한다고 할 때,
p의 확률로 A가 1달러를 더 얻고, q의 확률로 1달러를 잃는다.
0,N은 흡수상태(absorbing state)라고 하여, 게임 종료를 나타낸다.
\(p_i\): A가 i달러로 시작하여 게임을 이길 확률
\(p_i=p \cdot p_{i+1} + q \cdot p_{i-1}\), (1 <= i <= N-1)이고, \(p_0=0, p_N=1\)이다.
이를 Difference Equation이라고 한다.(미분 방정식의 이산형태, 계차방정식)
guessing을 통한 풀이
\(p_i = x^i\)라고 하자.
\[x^i = p x^{i+1} + q x^{i-1}\] \[px^2 - x + q = 0\]\(x=\frac{-1 \pm \sqrt{1-4pq}}{2p}\) 이고, \(q=1-p\)이기 때문에, \(1-4pq=(2p-1)^2\) 이 성립한다.
\[x \in 1, \frac{q}{p}\]두 해를 기저로하면
\[p_i = A \cdot 1^i + B \cdot \frac{q}{p}^i, (p \ne q)\]초기조건 \(p_0=0, p_N=1\)
어찌저찌 풀면
\[p_i=\frac{1-(\frac{q}{p})^i}{1-(\frac{q}{p})^{N-i}}, (p \ne q)\]그리고 p=q인 경우는 x->1 극한으로 보내면됨. 그러면,
\[p_i=\frac{i}{N}\]해석
공평한 상황이라고 해보자.
내가 돈을 i만큼 갖고 있을 때 승률은
\[p_i=\frac{i}{N}\]즉, 내가 상대보다 돈이 더 많으면 유리하다.
이는 50:50의 승률을 갖는 카지노일지라도 카지노에게 유리한 조건이라는 뜻이다.
Random Variable
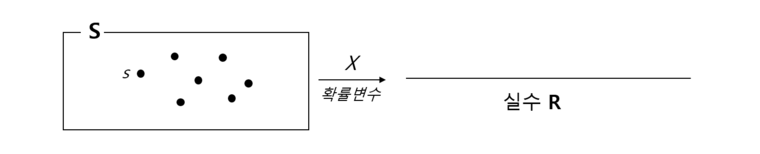
표본공간 S부터 실수 체계 R로 ‘맵핑’ 하는 함수
함수라고 했는데 random은 어디서 오는것인가?
Randomness는 함수 자체로부터 오는 것이 아니라 랜덤성을 지닌 사건으로부터 온다.
Bernoulli Random Variable
X가 0, 1 두가지의 값만 가질 수 있다.
0일 때 실패, 1일 때 성공으로 해석한다.
\(P(X=1)=p, P(X=0)=1-p\) 일 때,
X는 Bernoulli(p) 분포를 따른다고 한다.
Binomial Random Variable
n번의 독립적인 베르누이(p) 시행에서, 성공 횟수의 분포는 Bin(n,p)를 따른다고 한다.
Binomial R.V.의 PMF
\[P(X=k)=\binom{n}{k}p^k(1-p)^{n-k}\]Binomial R.V.의 특징
X~Bin(n,p), Y~Bin(m,p) 일 때,
X+Y~Bin(n+m,p)를 따른다.
Binomial Distribution
Bin(n,p)는 모수(parameter) n,p에 의해 분포가 결정된다.
Probability Distribution
Probability Distribution을 해석하는 방법
ex) X~Bin(n,p)
의미
n번의 독립적인 Bernoulli(p) 시행에서 성공한 횟수
지시확률변수(indicator random variables)
\(X=X_1+X_2+...+X_n\), \(X_1,...,X_n~^{iid}Bern(p)\)
\(X_j=\) 성공인 경우 1, 실패인 경우 0
확률질량함수(Probability Mass Function, PFM)
사건의 발생확률을 구할 수 있다.
\(P(X=k)=\binom{n}{k}p^k q^{n-k}\), (q=1-p)
누적분포함수(Cummulative Distribution Function, CDF)
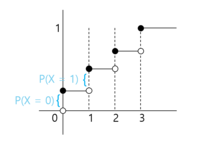
X <= x 이라는 사건에 대해 확률을 구한다.
\(F(X) = P(X<=x)\) 확률질량함수(이산확률변수에서만)
\(p_j=P(X=a_j)\) 조건: \(p_j>=0, \sum_j p_j=1\)
이항확률변수 PMF:
\(P(X=k)=\binom{n}{k}p^k q^{n-k}, k \in \{0,1,...,n\}\)
조건확인을 해보자
\[\sum_j p_j = \sum_{k=0}^n \binom{n}{k} p^k q^{n-k} = (p+1-p)^n = 1\]CDF의 필요충분조건
- 증가함수
- 우연속함수
- \( F(X) \rightarrow 0 \text{ as } X \rightarrow -\infty, F(X) \rightarrow 1 \text{ as } X \rightarrow \infty \)
이는 필요충분조건이다!
Hypergeometric, 복원 하지 않는 표본추출
5장의 카드를 덱에서 뽑을 때, 그 중 에이스 카드의 수
b개의 검정색 구슬과 w개의 흰색 구슬 중 n개의 표본을 무작위로 추출할 때, 표본에 있는 흰색 구슬의 수
위의 예제는 모두 초기하분포(hypergeometric distribution)를 따르며, 복원을 하지 않는 표본추출이라는 점에서 이항분포와 다르다.
그러나 표본공간이 매우 커서 복원 여부가 별로 차이가 나지 않는다면 이항분포에 근사한다.
Independence of r.v.s
연속확률변수
모든 x,y값에 대하여 \(P(X \le x, Y \le y)=P(X \le x)P(Y \le y)\) 등식이 성립할 때, 확률변수 X,Y가 독립이라고 할 수 있다.
이산확률변수
모든 x,y값에 대하여 \(P(X=x,Y=y)=P(X=x)P(Y=y)\) 등식이 성립할 때,
확률변수 X,Y가 독립이라고 할 수 있다.