Expectation
확률변수의 평균값이다.
그러나 동일하게 취급할지, 각각 서로 다르게 weight할지가 다르다.
Unweighted average
\[1,2,3,4,5,6 \rightarrow \frac{1+2+3+4+5+6}{6}\]Weighted average
\(1,1,1,1,1,3,3,5 \rightarrow \frac{5}{8} \times 1 + \frac{2}{8} \times 3 + \frac{1}{8} \times 5\)
각 가중치를 전부 더하면 1이 된다.
여기서 가중치는 확률이 된다.
Expectation of R.V
이산확률변수(discrete r.v)의 기댓값
\(E(X) = \sum_x XP(X=x),(P(X=x)>0)\)
\(\rightarrow \sum 값 * 확률질량함수\)
베르누이 확률변수(Bernoulli r.v)의 기댓값
\(X \sim Bern(p)\)
\(E(X)=1 \cdot P(X=1) + 0 \cdot P(X=0)=p\)
X=사건 A가 발생한 경우 1, 그 외의 경우 0
\(E(X)=P(A) \rightarrow\) X를 지시확률변수로 생각해 볼 수 있다.
이항 확률변수(Binomial r.v)의 기대값
\(X \sim Bin(n,p)\)
\(E(X)=\sum_{k=1}^{n}k \binom{n}{k} p^k q^{n-k}=\sum_{k=1}^{n} n \binom{n-1}{k-1} p^k q^{n-k}\)
\(=np \sum_{k=1}^n \binom{n-1}{k-1} p^{k-1}q^{n-k}\)
j=k-1이라고 하면,
\(=np \sum_{k=1}^n \binom{n-1}{j} p^{j}q^{n-1-j}\)
이항정리에 의해 \(\sum_{k=1}^{n} \binom{n-1}{j} p^j q^{n-1-j}=1\)
\(=np\)
기하확률변수(geometric random variable)
Geom(p): 여러 번의 Bern(p) 독립시행에서 첫 번째 성공까지의 실패 수
\(X \sim Geom(p),(q=1-p)\)라고 할 때,
X의 PMF:
\(P(X=k)=q^kp,(k \in \{0,1,...\})\)
조건확인: \(\sum_{k=1}^{\infty}pq^k = \frac{p}{1-q}=1\)
기하확률변수의 기댓값
\[E(X)=\sum_{k=0}^{\inf}k p q^k = p \sum_{k=0}^{\inf}k q^k\] \[\sum_{k=0}^{\infty} q^k = \frac{1}{1-q}\]이를 미분하면
\[\sum_{k=1}^{\infty} k q^{k-1}= \frac{1}{(1-q)^2}\] \[\rightarrow \sum_{k=1}^{\infty} k q^k = \frac{q}{p^2}\] \[\therefore E(X) = p \sum_{k=0}^{\infty} k q^k = p \cdot \frac{q}{p^2} = \frac{q}{p}\]Story proof 2강 이용하여 해석
\[c=E(X)\] \[c= 0 \cdot p + (1+c) \cdot q\] \[=q + cq\] \[c=\frac{q}{1-q}=\frac{q}{p}\]첫번째 성공(First Success) 분포
\[X \sim FS(p)\]\(Y=X-1\)이라 하였을 때, \(Y \sim Geom(p)\)
\[E(X)=E(Y)+1 \\\\ =\frac{q}{p}+1 = \frac{1}{p}\]무기억성
기하분포는 무기억성을 지닌다.
Poisson Distribution
\[X \sim Pois(\lambda )\]의미
굉장히 여러번의 시행을 하지만, 성공의 확률이 매우 낮을 때의 성공 횟수 세기.
ex) 한 시간 동안 오는 이메일의 갯수.
엄청나게 많은 수의 사건이 각각 독립적으로(혹은 약한 의존성으로) 매우 낮은 발생확률이 있을 때 사건이 발생한 갯수!
이는 큰 수의 이항분포와 근사한다.
PMF
\[P(X=k)=\frac{e^{-\lambda}\lambda^k}{k!},(k \in {0,1,2,...})\]\(\rightarrow \lambda\)는 속도를 나타내는 모수로, \(\lambda >0\) 인 상수이다.
조건확인: \(\sum_{k=0}^{\infty} \frac{e^{-\lambda} \lambda^k}{k!}=e^{-\lambda} e^{\lambda} = 1\)
테일러 시리즈에 \(e^{-\lambda}\) 를 곱하여 1로 만들어준것이다.
기댓값
\[E(X) = e^{-\lambda} \sum_{k=0}^{\infty}k \lambda^k / k!\] \[=\lambda e^{-\lambda} \sum_{k=1}^{\infty} \frac{\lambda^{k-1}}{(k-1)!}=\lambda e^{-\lambda} e^{\lambda}=\lambda\]평균이 모수 그자체다. 외우기 정말 쉽다.
Poisson approximation
어떤 큰 숫자 n에 대하여 \(A_1,...,A_n\)의 사건들이 각각 \(P(A_j)=p_j\)라는 낮은 확률로 발생하고, 각 사건이 독립이거나 weekly dependent할 때,
발생하는 사건(\(A_j\))의 수는 \(Pois(\lambda)\)의 분포를 따른다.
\[\lambda=\sum p_j\]또한 \(X \sim Bin(n,p)\)는 \(n \rightarrow \infty, p \rightarrow 0\)하고 \(np=\lambda\) 가 상수로 유지될 때 (n과 p가 증가하는 속도가 같음)
이항확률변수 X의 분포는 포아송에 근사하게 된다.
증명
\(n \rightarrow \infty\) 할 때 몇몇 성분들이 1로 수렴하면서
\[\binom{n}{k} p^k (1-p)^{n-k} \approx \frac{\lambda^k}{k!}e^{-\lambda}\]빗방울
길바닥에 빗방울이 떨어지는 횟수 또한 포아송 근사로 설명할 수 있다.
각 사각형에 빗방울이 떨어지는 사건은 이항분포이지만, 그 사건은 서로 독립이다.
빗방울은 많이 떨어지지만 한 사각형 안에 떨어질 확률은 작기 때문에, 포아송 분포로도 볼 수 있다.
기대값의 선형성(linearity)
- \(E(X+Y)=E(X)+E(Y) \rightarrow X,Y\)가 서로 독립이 아닌 경우에도 성립!
- \(E(cX)=cE(X)\), c는 상수
독립이 아니어도 성립하기 때문에 굉장히 유용하다.
선형성 증명
이산확률변수에 대해서.
\[\text{Let }T=X+Y\] \[\text{Show }E(T)=E(X)+E(Y)\] \[\rightarrow \sum_t t P(T=t) =^? \sum_x x P(X=x) + \sum_y y P(Y=y)\]위는 각각의 확률에 따라 weighted한 평균이다. t는 T의 possible value, x는 X의.. 그런식이다.
이것을 증명하기 위해선 두가지 방법이 있는데, 우측을 풀어 좌측과 같다는걸 보여주는거고, 좌측을 풀어 우측과 같다는것을 보여주는것이다.
조약돌 세계를 다시 생각해보자.
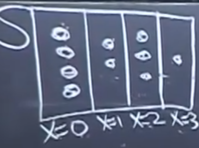
여기서 X의 possible value는 0,1,2,3으로 되어있지만 실제로는 어떤 값을 가져도 상관없다.
각각의 조약돌을 s라고 한다면,
\[E(X)=\sum_x xP(X=x)=\sum_s X(s)P(\{s\})\]두번째 식처럼 random variable에 대한 합을 구하는 것이 아니라,
각 조약돌에 대한 합을 구하는 것이다.
\(P(\{s\})\)는 조약돌의 질량을 의미한다.
둘의 차이는 random variable은 grouped되었다는 것이고,
조약돌은 ungrouped라는 것이다.
둘다 똑같은 weighted 평균이다.
Proof (discrete case)
\[E(T)=\sum_s(X+Y)(S)P(\{s\})=\sum_s(X(s)+Y(s))P(\{s\}) \\\\ =\sum_s X(s)P(\{s\}) + \sum_s Y(s)P(\{s\}) \\\\ =E(X)+E(Y)\]그래서 다음 식도 가능하다.
\(E(cX)=cE(X)\), c는 상수
이 식은 X=Y라는 가장 극단적인 종속 상황에서도 성립한다.
이항확률변수의 기댓값(선형성 이용)
\(X=X_1+...+X_n\)이기 때문에(\(X_i\)는 각각 베르누이 시행) \(E(X)=n \cdot E(X_1)=np\)
음이항분포(Negative Binomial)
\[NegBin(r,p)\]모수는 r,p이다.
의미
여러 번의 Bern(p) 독립시행 중에서 r번째 성공까지의 실패 횟수.
PMF
\[P(X=n)=\binom{n+r-1}{r-1}p^r q^n, n=0,1,2,...\]지시확률변수
Most simple case: r=1일 때, \(X \sim Geom(p)\)
\[E(X)=\frac{q}{p}\] \[E(X)=E(X_1+X_2+...+X_r)=E(X_1)+...+E(X_r)\]\(X_j\)는 j-1번째와 j번째 성공 사이의 실패 횟수라고 할 때,
\(X_j \sim Geom(p)\) 이므로
\[E(X)=r \times \frac{q}{p}\]