Change of Variables
\(X\)가 PDF \(f_x\)를 따르고.
\(Y=g(X)\) 일 때, (g는 미분가능한 단조증가함수)
\[f_Y(y)=f_X(x) \frac{dx}{dy} (y=g(x) \leftrightarrow x=g^{-1}(y))\]Multidimensional Transformation and Sum of Convolution
Shannon’s noisy Channel Coding Theorem
다음에
Beta Distribution
\[Beta(a,b) (a > 0, b > 0)\]PDF:
\[f(x) = c x^{a-1} (1-x)^{b-1},(0 < x < 1)\]a,b는 양의 실수인 파라미터이다. x는 0에서 1사이의 값.
c는 normalizing constant. PDF를 0부터 1까지 적분하여 값이 1이되도록 한다.
베타분포는 균등분포(uniform distribution)의 일반화와 같다.
지금까지 배운 분포중 연속적이고 유한한 것은 균등분포밖에 없었다.
베타분포는 여러 분포들의 집합이다.
매우 유연한 확률분포여서 a,b를 바꾸면서 형태를 바꿀 수 있다.
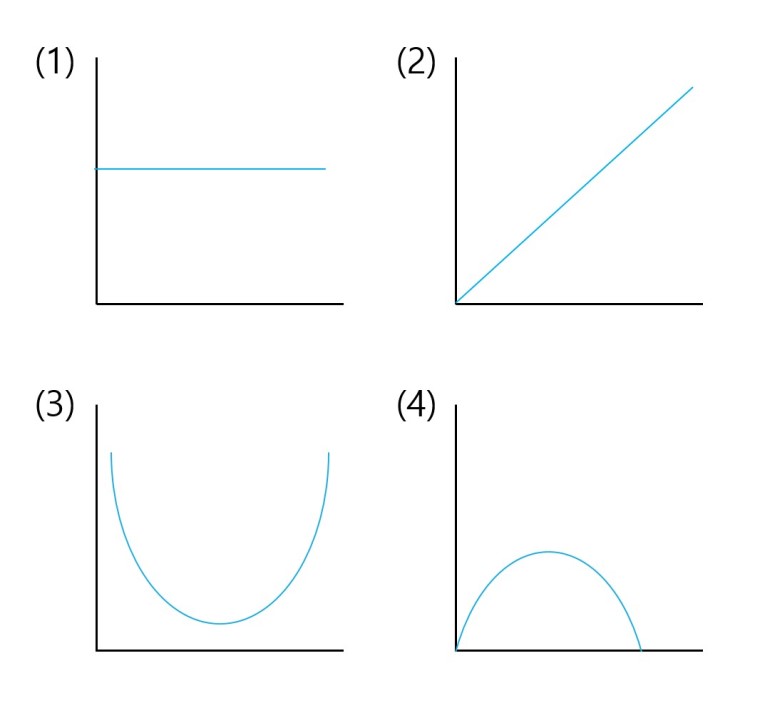
(1) a = b = 1인 경우
(2) a = 2, b = 1인 경우
(3) a = b = 1/2인 경우
(4) a= b= 2인 경우
1/2인 경우 (a-1)같은 것이 음수가 되어버리기 때문에 끝구간에서 무한대로 가게 된다.
1보다 큰 경우 끝구간에서 0으로 간다.
베타 분포는 이러한 특징 덕분에 확률에 대한 확률로 사용된다.
- 파라미터(모수)로 자주 쓰이고
- 이항분포에 켤레사전분포(conjugate prior)로 쓰이며 (파라미터는 0에서 1 사이)(likelihood가 Binom이면 conjugate는 Beta)
- 다른 분포와도 잘 연결된다.
이후 예제를 살펴보면서 베타분포를 익혀보자.
Laplace Rule of Succession and Bayes’ Billiards
Laplace Rule of Succession에서 binomial인 likelihood에 대해 beta인 prior는 posterior가 똑같이 beta분포이다.
직관적인 해석은 x가 성공한 횟수라고 했을 때, n-x는 실패한 횟수를 의미하는데,
실험전에 a번의 성공과 b번의 실패를 하였고, 추가된 성공과 실패에 대해서 분포를 새로 예측하는 것이다.
기대값과 분산
매우 간단하다.
x를 곱하면 여전히 베타분포고.
x 제곱을 곱해도 여전히 베타분포이다.
Gamma Function
0,1,2
다음에 뭐가 나올까?
많은 사람들이 3이라고 생각하지만
답은 720! 이란다.(?)
0, 1!, 2!!, 3!!!, 4!!!!, …
이러한 경우의 문제는 애매한데, 두 사람이 동의할만한 가장 간단한 답을 찾으려면 어떻게 해야할까?
우리가 만약 어떤 숫자들의 시퀀스를 가지고 있을 때, 다음 숫자를 어떻게 알 수 있을까?
스털링 근사식.
\[n! \sim \sqrt{2 \pi n} (\frac{n}{e})^n\]이 근사는 정말 뛰어나서 n!을 스털링 근사식으로 나누면 n이 무한대로 가면 ratio가 1이된다.
포아송을 이용해서 이를 사용할 일이 있을거다.
팩토리얼은 이산적인데, 그러면 점과 점사이를 연결하는 방법은 어떻게 생각하는게 좋을까.
당장 3!과 4! 사이를 연결하는 방법만 해도 무수히 많다.
이 문제에 대한 모범답안이 감마함수이다.ㅈ
베타를 이해하기 위해 감마를 이해해야한다.
수학에서 정말 유명한 함수이다.
감마함수는 a가 어떤 양의 정수일 때 팩토리얼식이 된다. 이는 팩토리얼을 양의 실수로 확장한다.
Gamma Distribution
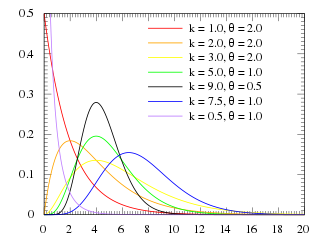
감마함수를 기반으로 PDF를 만드는 방법이있다.
PDF는 그냥 적분값이 1이면 된다. 그렇기 때문에 해당하는 감마 함수 값으로 그냥 나눠주면 된다.
감마분포는 지수함수와 연관성이 매우 높다.
지수함수와 매우 비슷하고 양의 실수에 대한 연속 분포이다.
많은 분포는 감마분포나 정규분포의 변형이다.
심지어 감마와 정규는 서로 연관성이 있다.
감마와 정규분포만 있으면 나머지에 대해선 거의다 만들어낼 수있다.
Poisson Process
감마분포와 지수분포가 연관이 있는 지점.
\(T_n:\) n번째 이메일이 도착한 시점

0과 t 시점 사이에, 첫 번째 이메일이 도착한 시점 T1
\(N_t:\) t 시점까지 도착한 이메일의 수 \(\sim Pois(\lambda t)\)
(서로 다른 시간 구간에 이메일은 서로 독립적으로 도착한다)
\[P(T_1 > t) = P(N_t =0) \\\\ =e^{-\lambda t}\]여기서 \(T_1\)까지 걸린 시간은 \(Exp(\lambda)\) 분포를 따름을 알 수 있다.

도착 시간 간격을 알고 싶은 것이 아니라 타임라인 상의 절대적 시간 그자체를 알고 싶다면,
\(T_n=\) (n번째 도착의 시간)
이는 이전의 도착 시간 간격을 전부 더한것과 같다.
Beta Distribution and Gamma Distribution