Inequalities
부등식과 근사는 다르다.
포아송 근사나 뒤에서 다룰 정규분포 근사같은것들과 다르다.
근사는 a < x < b 를 알고있어서 x의 대략적인 위치를 예상하는 것이라고 하면,
부등식은 x < b 인것만 알고있어서 정확한 위치를 알 수 없다.
그러나 부등식은 ‘증명’된 것이기 때문에 자명하다.
코시 슈바르트
E(XY)는 내적의 역할을 한다.
즉 내적은 두 길이의 곱보다 항상 작거나 같다.
만약 X와 Y가 uncorrelated면 E(XY)=E(X)E(Y)가 되어서 등식이된다.
\[E(X^2) \ge (E(X))^2\]\(X^2\)은 항상 양수이므로..
젠슨
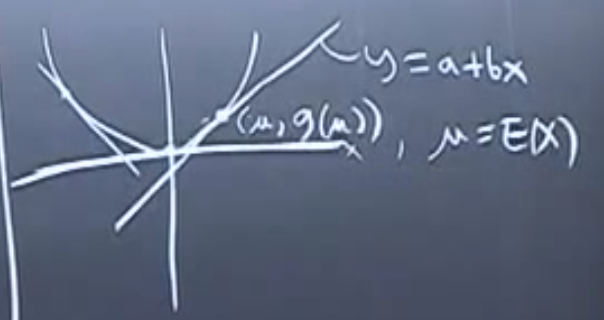
어떤 점에서 접선을 그어도 곡선보다 아래에 있다.
어떠한 X에 대해서도 곡선보다 아래에있다는 사실을 이용하자.
\[E(g(X)) \ge E(a+bX) = a+ bE(X) = a+b \mu\]테일러를 이용해서 증명하는 것도 가능하다.
마코프
체비셰프
Law of Large Numbers
\(X_1,...,X_n\) 이 i.i.d 하고 평균 \(/mu\), 표준편차 \(/sigma^2\)를 가질 때,
\(\bar{X_n}=\frac{1}{n} \sum_{j=1}^{n}X_j\) (표본평균) 이라고 정의하자.
Strong LLN
\(n \rightarrow \infty\) 에 따라 1의 확률로 \(\bar{X_n} \rightarrow \mu\) 한다.
즉 표본평균이 실제 모평균에 근사하게 된다는 것이다.
여기서 표본평균은 그냥 확률변수인데 실제 모평균은 상수이다.
ex) \(X_j \sim Bern(p)\) 일 때, 1의 확률로 \(\frac{X_1+...+X_n}{n} \rightarrow p\) 이다.
동전 던지기를 무한번 하게 되면 실제 확률로 수렴하는 것이다.
여기서 i.i.d라는 것은 매우 중요한 전제이다.
Weak LLN
| 모든 \(c > 0\)에 대하여 $$P( | \bar{X_n} = \mu | > c) \rightarrow 0 (n \rightarrow \infty)$$ |
확률이 수렴한다.
여기서 c는 어떤 작은 숫자.
| 증명) $$P( | \bar{X_n}-\mu | > c) \ge \frac{Var(\bar{X_n})}{c^2} = \frac{1}{n^2} n \sigma^2 \frac{1}{c^2} = \frac{\sigma^2}{nc^2} \rightarrow 0 (n \rightarrow \infty)$$ |
체비셰프 부등식으로 증명.
Central Limit Theorem
CLT는 표본평균과 평균의 차이를 적절히 스케일링 한 것이 표준 정규분포 모양으로 수렴한다는 것이다.
Chi-Square Distribution
\[\xi^2(n)\]여기서 n은 자유도인데, n을 생략하고 카이 제곱이라고 부른다.
아래 그림에서 결과는 \(Z \sim \xi^2\) 이 아니라
\[V \sim \xi^2(n)\]
student-t Distribution
Multivariate Normal
